Σάββατο 31 Μαΐου 2008
MAURICE SIDNEY BECK, F Inst P (1929-1999)
 After graduating with a 1st in Electrical Engineering from Leeds University in 1950, he pursued postgraduate studies at Imperial College. The research was concerned with servomechanisms and the then new work on time series analysis strongly influenced his future career.
After graduating with a 1st in Electrical Engineering from Leeds University in 1950, he pursued postgraduate studies at Imperial College. The research was concerned with servomechanisms and the then new work on time series analysis strongly influenced his future career.In 1952, he joined ICI as an instrument and electrical engineer. The Billingham plants at that time employed 20,000 people and processed many kinds of raw material. Maurice designed and maintained complex electronic systems for use in the extremely hostile on-site environment. In 1963 he moved to Bradford University to set up a new course: ‘Automation in Chemical Engineering’, and researched into the problems concerning measurement and control for processes handling difficult fluids, an endemic problem in his previous job. This progressed into an extensive programme of work on cross-correlation flowmeters and he was awarded his PhD in 1969, on the basis of this research. The textbook he wrote on the subject, (in collaboration with Andrzej Plaskowski) is well known to a generation of students.
In 1980, he became one of the founding professors of the new Department of Instrumentation and Analytical Science at UMIST. Here the research proceeded on a wider front, and in the mid-1980’s he became interested in using tomographic techniques to image process vessels and pipelines in order to obtain detailed information for design, measurement and control of multiphase processes. The differences from medical tomography soon became clear. Low-cost, safe, fast and highly sensitive tomographic sensors were required.
By 1989 a major effort was needed to develop process tomography to meet industrial needs. In that year Maurice Beck was awarded one of the few SERC Senior Fellowships so that he was able to work full-time on the subject. A Process Tomography Unit was set up in the Department of Electrical Engineering and Electronics at UMIST. This led to establishing a UK Process Tomography Group in 1990 and the foundation of a European Concerted Action in Process Tomography (ECAPT) in 1992. The UMIST group of 4 persons in 1990 soon expanded to a total of 30. ECAPT represented the output of 130 workers from over 40 groups (including 13 industrial groups) in 10 countries.
After its foundation in 1990 the UMIST group rapidly became world leaders in electrical tomography (using resistive, capacitive and inductive fields). The special features of high speed, low cost and safety attracted great interest in the form of research funding from many sources.
Maurice was a prodigious worker and this is reflected in his published output in the form of papers, books and edited conference proceedings. Although single minded in his enthusiasm for process tomography, he was never selfish. He was always ready to discuss ideas and exchange information in a way that, in the current climate, would not sit comfortably with the would-be exploiters of IPR. Nevertheless, he had an acute sense of the industrial need for technology transfer and was instrumental in setting up a commercial company to produce electrical tomographic systems. Undoubtedly, some other workers were able to capitalise on ideas gained through Maurice, but he felt that the excursions of the swings and roundabouts benefited him as well. His over-riding concern was that the subject should go forward and progress made.
Nor did his huge enthusiasm for process tomography mean that he neglected other aspects of his life. Home construction projects with his children, holidays in the caravan with his grandchildren, no one was left out. In later life, he took up jogging and, in his 60’s, took part in four London Marathons. More the tortoise than the hare, he always completed the course.
Maurice was held in the highest esteem by his peers and was awarded many honours and distinctions by professional and national institutions. In the technical world, he will be remembered as the Father of Process Tomography. To those of us who knew him well, he will be remembered as a kind generous and thoughtful gentleman, whose warm spirit and gifted leadership made us all feel proud to have known him.
Rolf Isermann, University of Darmstadt
 Rolf Isermann received the Dipl.-Ing degree in mechanical engineering in 1962 from the University of Stuttgart. With a thesis on the multivariable control of steam generators he received the Dr.-Ing. degree in 1965. In 1968 he became "Privatdozent" for automatic control at the University of Stuttgart and since 1972 Professor in Control Engineering. Since 1977 he is Professor at the Darmstadt University of Technology and head of the Laboratory of Control Engineering and Process Automation at the Institute of Automatic Control. 1989 R. Isermann received the Dr. h.c. (honoris causa) from L'Université Libre de Bruxelles and 1996 from the Polytechnic University in Bucharest. In 1996 he was awarded by the VDE-Ehrenring, the highest scientific award from Verband der Elektrotechnik und Informationstechnik. In September 1998 he was invited as Russel Severance Springer Professor in the Department of Mechanical Engineering at the University of California at Berkeley. MIT Technology Review Magazine awarded him to the Top Ten of emerging Technologies. R. Isermann has published books on Modeling of Industrial Processes (1971), Process Identification (1971, 1974, 1988), Digital Control Systems (1977, 1981, 1987) in different languages, Adaptive Control Systems (1992) together with K.-H. Lachmann and D. Matko, Supervision and Fault Diagnosis (1994) and Mechatronic Systems (1999). Current research concentrates in the fields of Identification with neural networks, non-linear digital control, intelligent control and model based methods of process fault diagnosis with applications for hydraulic and pneumatic servo systems, combustion engines, automobiles and mechatronic systems. Since 1975 he hold several chair positions in IFAC Technical Committees. In 1996 he was elected as Vice-President of IFAC and chair for the Executive Board, followed by chair of the Technical Board in 1999 until 2002. In 1979 he organized the 5th IFAC-Symposium on Identification and System Parameter Estimation in Darmstadt. For the 6th IFAC/IFIP-Conference on Digital Computer Applications to process Control 1980 in Düsseldorf, he chaired the International Program Committee. He acted as Chairman of the International Program Committee for the 10th IFAC-World-Congress in Munich 1987. Furtheron he was Chairman for the 1st IFAC-Symposium SAFERPROCESS, Baden-Baden, 1991 and the 1st IFAC-Conference on Mechatronic Systems, Darmstadt held in 2000.
Rolf Isermann received the Dipl.-Ing degree in mechanical engineering in 1962 from the University of Stuttgart. With a thesis on the multivariable control of steam generators he received the Dr.-Ing. degree in 1965. In 1968 he became "Privatdozent" for automatic control at the University of Stuttgart and since 1972 Professor in Control Engineering. Since 1977 he is Professor at the Darmstadt University of Technology and head of the Laboratory of Control Engineering and Process Automation at the Institute of Automatic Control. 1989 R. Isermann received the Dr. h.c. (honoris causa) from L'Université Libre de Bruxelles and 1996 from the Polytechnic University in Bucharest. In 1996 he was awarded by the VDE-Ehrenring, the highest scientific award from Verband der Elektrotechnik und Informationstechnik. In September 1998 he was invited as Russel Severance Springer Professor in the Department of Mechanical Engineering at the University of California at Berkeley. MIT Technology Review Magazine awarded him to the Top Ten of emerging Technologies. R. Isermann has published books on Modeling of Industrial Processes (1971), Process Identification (1971, 1974, 1988), Digital Control Systems (1977, 1981, 1987) in different languages, Adaptive Control Systems (1992) together with K.-H. Lachmann and D. Matko, Supervision and Fault Diagnosis (1994) and Mechatronic Systems (1999). Current research concentrates in the fields of Identification with neural networks, non-linear digital control, intelligent control and model based methods of process fault diagnosis with applications for hydraulic and pneumatic servo systems, combustion engines, automobiles and mechatronic systems. Since 1975 he hold several chair positions in IFAC Technical Committees. In 1996 he was elected as Vice-President of IFAC and chair for the Executive Board, followed by chair of the Technical Board in 1999 until 2002. In 1979 he organized the 5th IFAC-Symposium on Identification and System Parameter Estimation in Darmstadt. For the 6th IFAC/IFIP-Conference on Digital Computer Applications to process Control 1980 in Düsseldorf, he chaired the International Program Committee. He acted as Chairman of the International Program Committee for the 10th IFAC-World-Congress in Munich 1987. Furtheron he was Chairman for the 1st IFAC-Symposium SAFERPROCESS, Baden-Baden, 1991 and the 1st IFAC-Conference on Mechatronic Systems, Darmstadt held in 2000.Cross-Correlation Measurement Technology
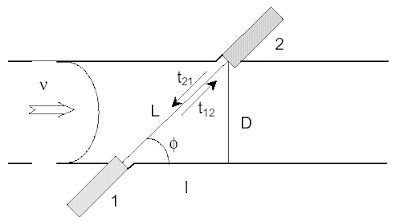
 A turbulent flow has a cascade structure of eddies. Along the flow, the characteristics of those structures do not change much within a certain distance, the so-called Correlation Length. In other words, turbulence at a certain distance apart are correlated. Based on this assumption, we can place two pairs of ultrasonic sensors along the flow direction to pick up the turbulence signature. Obviously, the upstream sensor will detect a flow signature L/V seconds earlier than the downstream one, where L is the space between the two sensors and V is the flow velocity. By comparing the signals from the two sensors, we are able to determine the time delay, thus, to calculate the velocity.
A turbulent flow has a cascade structure of eddies. Along the flow, the characteristics of those structures do not change much within a certain distance, the so-called Correlation Length. In other words, turbulence at a certain distance apart are correlated. Based on this assumption, we can place two pairs of ultrasonic sensors along the flow direction to pick up the turbulence signature. Obviously, the upstream sensor will detect a flow signature L/V seconds earlier than the downstream one, where L is the space between the two sensors and V is the flow velocity. By comparing the signals from the two sensors, we are able to determine the time delay, thus, to calculate the velocity.Cross-correlation-based technique used to estimate the time delay
Correlation peak detection (time-of-flight)
Properties of cross-correlation

The cross-correlation is related to the convolution by:
so that if either f or g is an even function
Also:
In analogy with the convolution theorem, the cross-correlation satisfies
where denotes the Fourier transform, and an asterisk again indicates the complex conjugate. Coupled with fast Fourier transform algorithms, this property is often exploited for the efficient numerical computation of cross-correlations.
The cross-correlation is related to the spectral density. See Wiener–Khinchin theorem
the cross correlation of a convolution of f and h with a function g is the convolution of the correlation of f and g with the kernel h:
so that if either f or g is an even function
Also:
In analogy with the convolution theorem, the cross-correlation satisfies
where denotes the Fourier transform, and an asterisk again indicates the complex conjugate. Coupled with fast Fourier transform algorithms, this property is often exploited for the efficient numerical computation of cross-correlations.
The cross-correlation is related to the spectral density. See Wiener–Khinchin theorem
the cross correlation of a convolution of f and h with a function g is the convolution of the correlation of f and g with the kernel h:
Correlation between Two Finite Signals
Algorithm 2:
Define x(n)
Define y(n)
Rotate (that is reverse) the signal h(n) using the MATLAB function fliplr(h) where h is to be flipped (i.e, rotated).
Find the convolution between x(n) and flipped version of h(n).
Plot the resultant signal
Program
% Program to find correlation of two signals
x=input ('Enter the first sequences x(n) : ');
h=input(' Enter the second sequences h(n) : ');
n1 =length(x)-1;
n2=length(h)-1;
r=conv(x,fliplr(h));
t=(-n1):n2;
stem(t,r);
xlabel(' lag index ');
ylabel(' Amplitude ');
v=axis;
axis([-n1 n2 v(3:end)]);
-------------------------------------------------------------------
Define x(n)
Define y(n)
Rotate (that is reverse) the signal h(n) using the MATLAB function fliplr(h) where h is to be flipped (i.e, rotated).
Find the convolution between x(n) and flipped version of h(n).
Plot the resultant signal
Program
% Program to find correlation of two signals
x=input ('Enter the first sequences x(n) : ');
h=input(' Enter the second sequences h(n) : ');
n1 =length(x)-1;
n2=length(h)-1;
r=conv(x,fliplr(h));
t=(-n1):n2;
stem(t,r);
xlabel(' lag index ');
ylabel(' Amplitude ');
v=axis;
axis([-n1 n2 v(3:end)]);
-------------------------------------------------------------------
Correlation between Two Finite Signals
Algorithm 1:
Cross correlation is defined as, if x(n) and h(n) are finite signals then cross correlation
In cross correlation folding of h(n) doesn’t occur.
Input the first sequence.
Input the second sequence
3. Find the cross correlation of these sequences using the MATLAB function "xcorr(x,h)" where x and h are the sequences to be correlated.
Plot the result
Program
% Program to find correlation of two signals
x=input ('Enter the first sequences ');
h=input(' Enter the second sequences ');
c= xcorr(x,h);
t=0 : (length(x) +length(h)-2);
stem(t,c);
-------------------------------------------------------------------
Cross correlation is defined as, if x(n) and h(n) are finite signals then cross correlation
In cross correlation folding of h(n) doesn’t occur.
Input the first sequence.
Input the second sequence
3. Find the cross correlation of these sequences using the MATLAB function "xcorr(x,h)" where x and h are the sequences to be correlated.
Plot the result
Program
% Program to find correlation of two signals
x=input ('Enter the first sequences ');
h=input(' Enter the second sequences ');
c= xcorr(x,h);
t=0 : (length(x) +length(h)-2);
stem(t,c);
-------------------------------------------------------------------
Παρασκευή 30 Μαΐου 2008
What is Cross Correlation
In signal processing, the cross-correlation is a measure of similarity of two signals, commonly used to find features in an unknown signal by comparing it to a known one. It is a function of the relative time between the signals, and has applications in pattern recognition and cryptanalysis. For discrete functions x(t) and y(t) the crosscorrelation is defined as:
What is the difference between cross-correlation and convolution
The cross-correlation is similar in nature to the convolution of two functions. Whereas convolution involves reversing a signal, then shifting it and multiplying by another signal, correlation only involves shifting it and multiplying (no reversing).
Σάββατο 24 Μαΐου 2008
Εγγραφή σε:
Σχόλια (Atom)