Basic time-of-flight measurement principle.

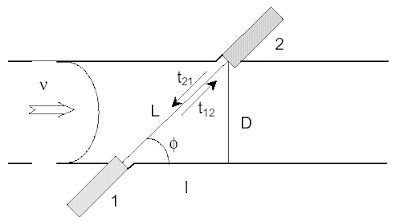
Correlation peak detection (time-of-flight)

The resulting signal peak of a correlation between a transmitted signal and a pulse-compressed reference signal at the receiver. Peak-detection determines, the time-of-flight.

Clamp on Sensors

Clamp on flowmeters

Properties of cross-correlation

Properties of cross-correlation

The cross-correlation is related to the convolution by:
so that if either f or g is an even function
Also:
In analogy with the convolution theorem, the cross-correlation satisfies
where denotes the Fourier transform, and an asterisk again indicates the complex conjugate. Coupled with fast Fourier transform algorithms, this property is often exploited for the efficient numerical computation of cross-correlations.
The cross-correlation is related to the spectral density. See Wiener–Khinchin theorem
the cross correlation of a convolution of f and h with a function g is the convolution of the correlation of f and g with the kernel h:

Correlation between Two Finite Signals

Algorithm 2:
Define x(n)
Define y(n)
Rotate (that is reverse) the signal h(n) using the MATLAB function fliplr(h) where h is to be flipped (i.e, rotated).
Find the convolution between x(n) and flipped version of h(n).
Plot the resultant signal
Program
% Program to find correlation of two signals
x=input ('Enter the first sequences x(n) : ');
h=input(' Enter the second sequences h(n) : ');
n1 =length(x)-1;
n2=length(h)-1;
r=conv(x,fliplr(h));
t=(-n1):n2;
stem(t,r);
xlabel(' lag index ');
ylabel(' Amplitude ');
v=axis;
axis([-n1 n2 v(3:end)]);
-------------------------------------------------------------------